計算機で何ができるのか

2025年3月15日

おはようございます。Yです。
これから、コンピュータすなわち計算機を使って何ができるのかを考えていきたいと思います。

まず、「言語」というものを考えます。我々が計算機を使うとき、計算機に対して指示を出す、つまり入力を与えるわけですが、この入力の方法を決めるわけです。日本語等の自然言語は、多義的であいまいな表現しかできない場面があったりして、これをそのまま入力で使おうとすると往々にして困難が生じます。それに対して、あいまいにならないように形式的に定義された言語は形式言語と呼ばれます。これは計算機について考察するために都合よく考えられたものだと思って構いません。もちろん自然言語で入力する方法も考えられ、実際にそれができるAIが世に登場したりしていますが、これからの議論はそれの基礎となるものです。

定義：
形式言語論において、言語は「単語」の集合です。
単語は、有限個の「アルファベット」の列です。
そして、アルファベットは、有限個の記号の集合です。

例1：
下記の$\Sigma_1$、$\Sigma_2$はアルファベットの例です。
\begin{equation}
\begin{split}
\Sigma_1 &= \{a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t, u, v, w, x, y, z\} \\
\Sigma_2 &= \{ご, す, り, ん\}
\end{split}
\end{equation}
$\Sigma_1$はいわゆる英語のアルファベットですが、形式言語論でのアルファベットという概念はもっと広いもので、$\Sigma_1$はその1つという扱いになります。
「りんご」「すりりんご」「ごりごり」は$\Sigma_2$上の単語です。
「ごりら」は$\Sigma_2$上の単語ではありません。
「apple」は$\Sigma_1$上の単語ですが、$\Sigma_2$上の単語ではありません。

例2：
下記の$L_1$は、「りんご」と「りす」の2つのみ単語をもつ言語です。
$$
L_1=\{りんご, りす\}
$$
例えば、「ごりら」や「すりりんご」は$L_1$に含まれないため、言語$L_1$の単語ではありません。

例3：
下記の$L_2$は日本語を形式的に表すことを試みています。
$$
L_2=\{わたし, は, りんご, です, …\}
$$
…には、活用形を含めた日本語の単語がすべて含まれます。
例えば「ごりら」は$L_2$に含まれますが、「apple」や「まそっぷ」は$L_2$に含まれません。

次に、入力された単語をどのように処理するかを、すなわち計算モデルを考えたいのですが、話を単純化するためにまず計算の機能を絞ります。
ここでは、単語を入力されたときに、その単語が特定の言語に含まれているかどうかを判定する計算機を考えます。

具体的に、単語が$L_1$に含まれているかどうかを判定する処理を作ったので、図を見ていただきましょう。

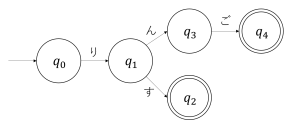
これに、「りんご」を入力したときの処理を説明します。
最初に、あなたは$q_0$のマルの中に居ると思ってください。
まず、入力の1文字目「り」を受け取りました。$q_0$からは「り」のラベルが付いた矢印があるので、その先の$q_1$に移動します。
次に、入力の2文字目「ん」を受け取りました。$q_1$からは「ん」のラベルが付いた矢印があるので、その先の$q_3$に移動します。
次に、入力の3文字目「ご」を受け取りました。$q_3$からは「ご」のラベルが付いた矢印があるので、その先の$q_4$に移動します。
ここで、入力が終わりました。あなたは二重マルが付いた場所にいるので、YESを返します。

また、「りん」を入力したときの処理を説明します。
まず、入力の1文字目「り」を受け取りました。$q_0$からは「り」のラベルが付いた矢印があるので、その先の$q_1$に移動します。
次に、入力の2文字目「ん」を受け取りました。$q_1$からは「ん」のラベルが付いた矢印があるので、その先の$q_3$に移動します。
ここで、入力が終わりました。あなたは二重マルが付いていない場所にいるので、NOを返します。

もう一つ、「ごりら」を入力したときの処理を説明します。
まず、入力の1文字目「ご」を受け取りました。$q_0$からは「ご」のラベルが付いた矢印がないので、NOを返します。

いかがでしょうか。この処理は、「りんご」か「りす」のいずれかを入力された時のみYESを返すことがわかると思います。この処理体系は「（決定性）有限オートマトン」と呼ばれる計算モデルで、私はこれを用いて$L_1$を判定するプログラムを書いたことになります（本当は有限オートマトンの形式的な定義をすべきですが、割愛させていただきます）。$L_1$に限らず、他の言語を判定する有限オートマトンを書くこともできます。

興味のある方は、下記の言語を判定する有限オートマトンを考えてみてください。
\begin{equation}
\begin{split}
L_3 &= \{りんご, すりりんご\} \\
L_4 &= \{ごり,ごりごり,ごりごりごり,ごりごりごりごり, …\}
\end{split}
\end{equation}
さて、有限オートマトンでプログラムが書けることは分かったのですが、現実に有限オートマトンを仕事で書いているプログラマはまず居ません。理由はたくさんありますが、その一つは有限オートマトンがC言語等のメジャーな処理体系に能力で劣っているからです。これについてはまた別の機会に堀り下げていきたいと思います。

それでは。